Lyapunov-Perron method

AAU

Chafee-Infante equation: Consider the nonautonomous Chafee-Infante equation

in one spatial dimension equipped with homogenous Dirichlet boundary condtions. The time-dependent coefficients are asymptotically autonomous

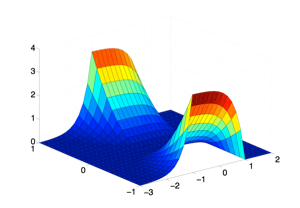
and for an appropriate choice of the sufficiently small parameter δ>0 there exists a 2-dimensional inertial manifold for the above nonlinear heat equation. The following animation illustrates the time-dependence of this inertial manifold for values t=-10...10. More precisely, we plotted the projection of the inertial manifold onto the first Fourier modes:

Inertial manifolds

(cf. Pötzsche and Rasmussen: Computation of nonautonomous invariant and inertial manifolds, Numerische Mathematik 112, 449-483, 2009)

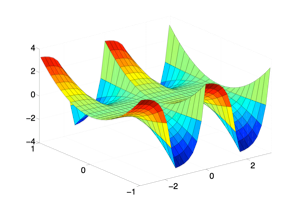
Henon map: A combination of pseudo-arclength continuation and our truncated Lyapunov-Perron approach can be applied to approximate the unstable manifold of the Henon map

and led to the following animation:

Unstable manifolds

(cf. Pötzsche and Rasmussen: Computation of nonautonomous invariant and inertial manifolds, Numerische Mathematik 112, 449-483, 2009)

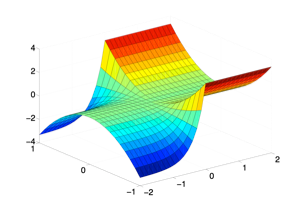
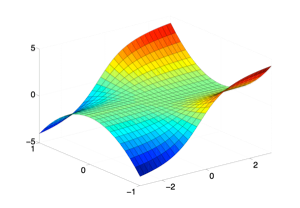
Stable integral manifolds

(cf. Pötzsche and Rasmussen: Computation of integral manifolds for Carathéodory differential equations, IMA Journal of Numerical Analysis 30(2), 401-430, 2010)

SIRS epidemic model: The following graphics show stable integral manifolds for a nonautonomous differential equations

with piecewise continuous time-dependence

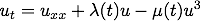
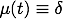
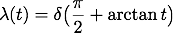
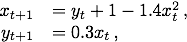
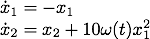
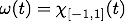
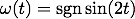
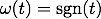
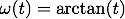
Christian Pötzsche (Feb 2011)